7.14 Exercícios
- Crie um vetor com os valores de \(e^{x}cos{x}\) para os valores de \(x = (3, 3.1, 3.2, ..., 6\)).
- Crie os seguintes vetores.
\((0.1^{3}\times0.2^{1}, 0.1^{6}\times0.2^{4}, ..., 0.1^{36}\times0.2^{34})\)
\((2, \frac{2^{2}}{2}, \frac{2^{3}}{3}, ..., \frac{2^{25}}{25})\)
- Reproduza a criação do vetor dias da semana (
dds) mostrado abaixo.
domingo segunda terca quarta quinta sexta sabado
1 2 3 4 5 6 7- Interprete o resultado da seguinte operação:
dds_nums <- c(
5L, 2L, 5L, 2L, 7L, 7L, 2L,
6L, 6L, 3L, 7L, 1L, 2L, 2L,
5L, 7L, 3L, 2L, 6L, 4L, 1L
)
names(dds)[dds_nums]- Escreva o código necessário para determinar o vetor lógico indicando quais números são pares na sequência de valores 85, 79, 70, 6, 32, 8, 17, 93, 81, 76. b. Calcule o total de números ímpares.
- Para um ano ser bissexto, ele deve ser:
divísivel por 4 (a divisão é exata com resto igual a zero)
não pode ser divisível por 100 (a divisão não é exata, ou seja, o resto é diferente de zero)
pode ser que seja divisível por 400: caso seja divisível por 400, a divisão deve ser exata, deixando o resto igual a zero.
Com os critérios definidos acima, construa o código para:
Verificar se os anos 1894, 1947, 1901, 1992, 1925, 2014, 1993, 1996, 1984, 1897, 2100, 2300 são bissextos.
Mostre quais anos são bissextos.
Usando o código para verificar se o ano é bissexto, gere um vetor nomeado
ndiascom o número de dias do ano para os anos do item (a).Programe como obter o total de anos com 366 dias?
- Quais códigos para gerar os seguintes dados:
[1] -30 0 5 10 15 20 30[1] 1.0 0.8 0.6 0.4 0.2 0.0[1] -3.1415927 -2.4434610 -1.7453293 -1.0471976 -0.3490659 0.3490659
[7] 1.0471976 1.7453293 2.4434610 3.1415927[1] -1 -1 0 0 0 1 1 1 1 2 2 2 2 2 3 3 3 3 3 3 4 4 4
[24] 4 4 4 4 5 5 5 5 5 5 5 5[1] 5 5 5 5 5 4 4 4 4 3 3 3 2 2 1 2 2 3 3 3 4 4 4 4 5 5 5 5 5- Usando o mesmo código para solução em todos os itens abaixo, obtenha as seguintes sequências usando os vetores fornecidos.
- v3 = (11, 0.25, 7, 2)
[1] 1 2 3 4- v2 = (11, 0.25)
[1] 1 2- v1 = (11)
[1] 1- v0 = ()
integer(0)- Considere os seguintes dados horários de temperatura do ar (\(T_{ar}\)) registrados em duas estações meteorológicas, entre as 0 e 23 horas de um dado dia.
tar_est1 <- c(
14.92, 14.61, 14.32, 14.07, 13.84, 13.65, 13.56, 13.97, 15.08,
16.5, 17.88, 19.08, 20.02, 20.66, 21.01, 21.05, 20.76, 20.05,
18.77, 17.51, 16.67, 16.11, 15.66, 15.27
)
tar_est2 <- c(
13.13, 13.01, 12.93, 12.87, 12.82, 12.81, 13.2, 14.22, 15.77,
17.49, 19.2, 20.57, 21.49, 22.01, 22.03, 21.71, 20.84, 18.77,
16.54, 15.13, 14.34, 13.81, 13.49, 13.28
)Dica: Faça um gráfico para visualizar as temperaturas das duas estações. Isso facilitará a solução.
a. Determine a média diária da \(T_{ar}\) das duas estações arrendondando para uma casa decimal. Salve a média de cada estação nas variáveis tmed_est1 e tmed_est2.
b. Utilizando as variáveis do item anterior, verifique usando comparação lógica, em qual estação o ambiente é mais quente?
c. Obtenha a 3ª maior temperatura do dia em cada estação.
d. Calcule a amplitude térmica diária (\(ATD = T_{max}-T_{min}\), onde \(T_{max}\): temperatura máxima dária e \(T_{min}\): temperatura mínima dária) das estações 1 e 2, arrendondando para uma casa decimal. Salve os resultados nas variaveis atd_est1 e atd_est2.
e. Qual o horário de ocorrência das temperaturas máximas e mínimas em cada estação? Salve os resultados nas variáveis hmax_est{i} e hmin_est{i}, com \(i = 1, 2\).
f. Quando tar_est2 é maior que tar_est1 qual a maior diferença absoluta de temperatura entre as duas estações?
g. Qual a hora correspondende a ocorrência daquela maior diferença absoluta de temperatura obtida no item anterior?
h. O horário do pôr do sol pode ser estimado a partir da \(T_{ar}\). Para o período após o horário de ocorrência da \(T_{max}\) determina-se em qual hora ocorre a maior queda de \(T_{ar}\) em relação a hora anterior. Estime o horário do pôr do sol para as duas estações (hps_est{i}).
i. Em quais horas as temperaturas das duas estações estão mais próximas uma da outra, ou seja com menos de 0,5°C de diferença ?
j. Calcule a temperatura média diária usando os seguintes métodos para estação 2.
\(T_{med_{1}} = (T_{max} + T_{min})/2\), salvando em uma variável tar_met1.
\(T_{med_{2}} = (T_{max} + T_{min} + T_{9} + 2T_{21})/5\), salvando em uma variável tar_met2.
\(T_{med_{3}} = (T_{7} + T_{14} + 2T_{21})/4\), salvando em uma variável tar_met2.
k.Compare este resultados com aqueles obtidos no item a. Qual é melhor?
- Calcule a temperatura do ar horária usando o modelo de onda para representação do ciclo diário da temperatura do ar, descrito pelas seguintes equações:
\[\left\{\begin{matrix} h_{T_{min}}\leq h < h_{T_{max}}, & T_{calc} = \bar{T} - A \, cos\left ( arg \right )\\ demais\; horas, & T_{calc} = \bar{T} + A \, cos\left ( arg \right ) \end{matrix}\right.\]
onde:
\[\bar{T} = \left ( \frac{T_{max} + T_{min}}{2} \right )\]
e
\[A =\left ( \frac{T_{max}-T_{min}}{2} \right ) \]
O argumento do cosseno (\(arg\)) é definido por:
\[\left\{\begin{matrix} h < h_{T_{min}}, & arg = \pi \left ( \frac{h+10}{10+h_{Tmin}} \right )\\ h_{T_{min}}\leq h < h_{T_{max}}, & arg = \pi \left ( \frac{h-h_{T_{min}}}{14-h_{T_{min}}} \right )\\ h > h_{T_{max}}, & arg = \pi\left ( \frac{14-h}{10+h_{Tmin}} \right ) \end{matrix}\right. \]
a. Aplique o método acima para estação 1 e 2 substituindo os valores de \(T_{max}\), \(T_{min}\), \(h_{T_{max}}\), \(h_{T_{max}}\), adequadamente.
b. Calcule o RMSE nos dois casos. \(RMSE = \sqrt{\frac{1}{n}\sum_{i=1}^{n}\left (T_{calc}-T_{obs} \right )^{2}}\)
c. Calcule a correlação (\(r\)) nos dois casos. A barra representa a média aritmética. Confira seu resultado com a saída da função cor(tar_obs, tar_calc).
\[r = \frac{\sum_{i=1}^{n} (T_{obs}-\bar{T}_{obs})(T_{calc}-\bar{T}_{calc}))}{\sqrt{\sum_{i = 1}^{n} (T_{obs}-\bar{T}_{obs})^{2}(T_{calc}-\bar{T}_{calc})^{2})}}\]
- Os dados abaixo são de precipitação horária de um evento severo ocorrido em 03/12/2012 em Santa Maria-RS.
| hora | prec |
|---|---|
| 9 | 0.0 |
| 10 | 0.0 |
| 11 | 0.0 |
| 12 | 0.0 |
| 13 | 0.0 |
| 14 | 0.0 |
| 15 | 0.0 |
| 16 | 21.4 |
| 17 | 41.2 |
| 18 | 2.6 |
| 19 | 1.0 |
| 20 | 0.4 |
| 21 | 0.0 |
Como seria o código para determinar a soma cumulativa da precipitação horária? Salve o resultado em um vetor chamado
prec_acum. Interprete o resultado dec(NA, diff(prec_acum)).Mostre o código para encontrar o horário de ocorrência da precipitação máxima?
Mostre o código para obter a hora de início e fim do evento de precipitação severa. Qual foi a duração do evento?
Qual foi a precipitação total do evento? Quanto da precipitação total do evento, em %, ocorreu até às 17 h?
- Considere o vetor
xdefinido pelos números descritos abaixo. Mostre como encontrar o primeiro número positivo localizado após o último número negativo. Por exemplo, seja o vetorzdefinido pelos valores (11, 10, 15, 2, 6, -15, -10, -22, -8, 5, 7, 2, 12, 8, 4, 1, 3, -3, -1, 30, 14). Os valores selecionados seriam 5 e 30.
- Considerando o vetor
preccom valores de precipitação diária indicado abaixo. Escreva o código para resolver as seguintes tarefas.
prec <- c(
0, 0, 0, 0.8, 0, 0.01, 0.75, 0,
0, 0, 0, 0.35, 0.08, 0, 0, 0, 0, 0.31, 0, 3.57, 12.17, 0, 0,
0, 0.04, 3.16, 0, 0.95, 0.79, 0, 0, 0, 0, 0, 3.51, 0, 0, 0.16,
0, 0, 8.16, 0.54, 4.39, 1.24, 0, 0, 0, 0, 0, 2.43, 0, 0, 0, 0,
0, 7.18, 0, 0, 0.26, 0, 0, 0.28, 0, 0, 0.09, 0.38, 0, 0, 0, 0,
0, 0, 0.51, 0, 0, 0, 0, 0, 0, 0.67, 0, 0, 0, 0, 0.15, 0, 0.82,
0, 0, 0, 0, 0, 0, 0, 0, 0.37, 0, 0.58, 4.95, 0, 0, 0, 0, 0, 7.68,
0, 0, 0.37, 0, 1.56, 0, 0, 0, 0.34, 0.48, 0, 4.21, 2.28, 4.3,
0, 3.38, 0, 0, 0, 0, 7.28, 0, 4.89, 3.91, 0, 0, 0, 0, 0, 0, 2.93,
0, 2.49, 0.77, 0, 2.9, 3.53, 0.83, 0, 0, 0, 0.94, 0.59, 0, 0,
0, 0, 0.04, 0, 0.65, 0, 0, 0, 6.23, 0.09, 0, 0.66, 0, 0, 0, 4.42,
0, 0, 0, 0.84, 0, 0, 0, 0, 0, 0.09, 0, 0, 0.08, 0, 0.66, 0, 0,
0, 0.06, 0, 0, 0, 3.28, 0, 0.8, 5.69, 0.8, 0
)Quantos dias ocorreram no intervalo 0 < prec < 0.25?
Substitua os valores de chuva registrados no intervalo 0 < prec < 0.25 por 0.
Crie um vetor denominado
prec01indicando o estado da precipitação (chuvoso = 1, seco = 0) baseado no limiar de 0.25 mm para detecção de chuva pelo pluviômetro.Qual a probabilidade de chuva dessa série de precipitação diária?
Qual a probabilidade de chover dois dias consecutivos (
p11)? Calcule a probabilidade de chover em qualquer um de dois dias consecutivos (p01 + p10)?Determine a duração de cada evento chuvoso (número de dias consecutivos).
O resultado esperado é um vetor que identifique o evento e sua duração.
duracao <- c(evento1 = 1, evento2 = 1, evento3 = 1, evento4 = 1, evento5 = 2,
evento6 = 1, evento7 = 2, evento8 = 1, evento9 = 4, evento10 = 1,
evento11 = 1, evento12 = 1, evento13 = 1, evento14 = 1, evento15 = 1,
evento16 = 1, evento17 = 1, evento18 = 1, evento19 = 2, evento20 = 1,
evento21 = 1, evento22 = 1, evento23 = 2, evento24 = 3, evento25 = 1,
evento26 = 1, evento27 = 2, evento28 = 1, evento29 = 2, evento30 = 3,
evento31 = 2, evento32 = 1, evento33 = 1, evento34 = 1, evento35 = 1,
evento36 = 1, evento37 = 1, evento38 = 1, evento39 = 3)duracao
#> evento1 evento2 evento3 evento4 evento5 evento6 evento7 evento8
#> 1 1 1 1 2 1 2 1
#> evento9 evento10 evento11 evento12 evento13 evento14 evento15 evento16
#> 4 1 1 1 1 1 1 1
#> evento17 evento18 evento19 evento20 evento21 evento22 evento23 evento24
#> 1 1 2 1 1 1 2 3
#> evento25 evento26 evento27 evento28 evento29 evento30 evento31 evento32
#> 1 1 2 1 2 3 2 1
#> evento33 evento34 evento35 evento36 evento37 evento38 evento39
#> 1 1 1 1 1 1 3- Dado o vetor
dadosmostrado abaixo.
dados <- c(
NA, NA, 27L, 7L, 4L, 0L, 26L, 15L, 25L, NA, NA, NA, NA, 6L,
29L, 18L, 17L, 23L, 20L, 1L, 30L, 13L, NA, NA, NA, NA, NA, NA,
NA, 19L
)Como você pode codificar a obtenção de um vetor com zeros nos valores válidos e com números sequenciais dentro das falhas?
Como a partir do vetor resultante do item anterior você pode obter um vetor cujo os valores dentro das falhas indique a ordem de ocorrência da falha.
Qual o código para determinar o tamanho de cada falha?
Como determinar o tamanho da maior falha?
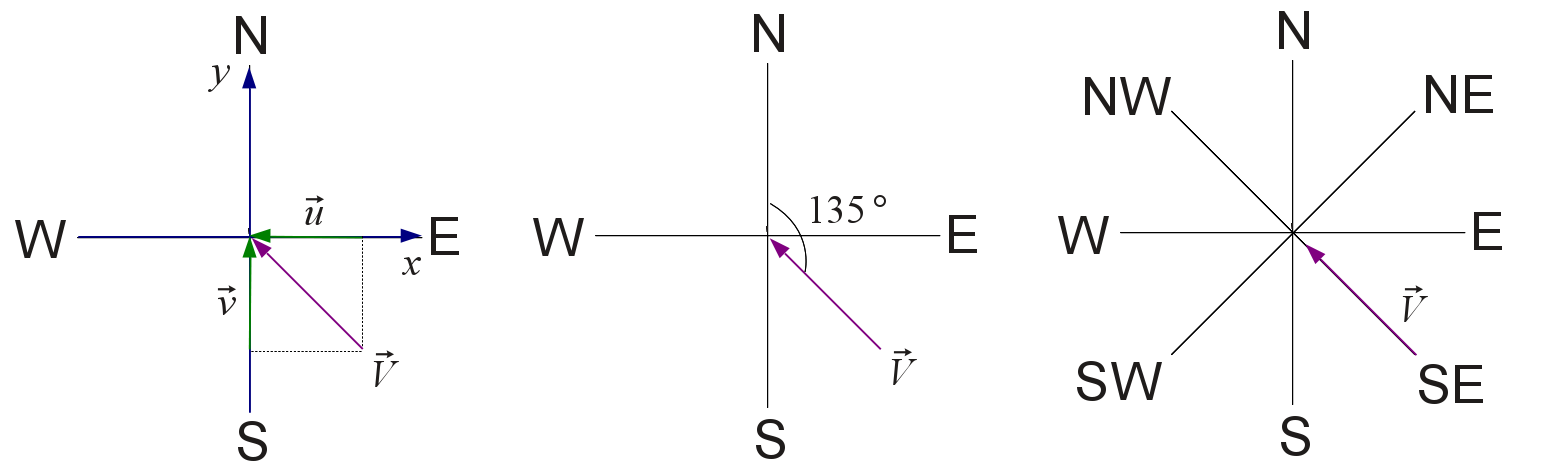
- Para os valores de velocidade (\(V_h\)) e a direção do vento (\(\theta\)) (na convenção meteorológica):
\(V_h\) = (10, 10, 10, 10, 14.142, 14.142, 14.142, 14.142, 0)
\(\theta\) = (270, 180, 360, 90, 225, 315, 135, 45, 0)
- Determine as componentes zonal e meridional do vento.
\[u = -V_{h} \cdot sin(\theta_{rad})\] \[v = -V_{h} \cdot cos(\theta_{rad})\]
- Faça os cálculos necessários para reconstruir \(V_h\) e \(\theta\), a partir de \(u\) e \(v\) determinados no item a. Por convenção, a direção do vento \(\theta\) em condições calmas (\(V_h\) < 0.5 m s-1) é assumida como 0°.
\[V_{h} = \sqrt{(u^2 + v^2)}\] \[\theta_{mat} = {\rm atan2}(-u, -v)\cdot\frac{180}{\pi}\] \[ \theta = \left\{\begin{matrix} \theta_{mat} + 360 & se & \theta_{mat} < 0 \\ 0 & se & u = 0,\: v = 0 \: \: ou \: \: V_{h} < 0.5\\ \end{matrix}\right. \]
A tabela abaixo apresenta o resultado esperado para as variáveis derivadas.
| u | v | ws | wd | wd_uv | dir |
|---|---|---|---|---|---|
| 10 | 0 | 10.000 | 270 | 270 | Oeste |
| 0 | 10 | 10.000 | 180 | 180 | Sul |
| 0 | -10 | 10.000 | 360 | 360 | Norte |
| -10 | 0 | 10.000 | 90 | 90 | Leste |
| 10 | 10 | 14.142 | 225 | 225 | Sudoeste |
| 10 | -10 | 14.142 | 315 | 315 | Noroeste |
| -10 | 10 | 14.142 | 135 | 135 | Sudeste |
| -10 | -10 | 14.142 | 45 | 45 | Nordeste |
| 0 | 0 | 0.000 | 0 | 0 | Calmo |
Dica: ver figura abaixo.
Para as séries de
prec_obseprec_simcalcule:A proporção corretamente prevista \(PC = \frac{wc+dc}{n}\)
O índice de sucesso crítico \(CSI=\frac{wc}{wc+wi+di}\).
Onde \(wc\) e \(dc\) são as previsões corretas de dias úmidos (\(prec > 0.25\) mm dia-1) e secos respectivamente, \(wi\) e \(di\) são as previsões incorretas de dias úmidos e secos respectivamente. \(n\) é o n° total de previsões.
prec_obs <- c(
0, 0, 0, 0.5, 1, 6, 9, 0.2, 1, 0, 0, 0.25,
10, 15, 8, 3, 0, 0, 0, 0, 0, 0, 0.25, 0,
0, 0, 1, 5, 0, 20, 0, 0, 0, 0, 1, 1,
0, 2, 12, 1, 0, 0, 0, 0, 0, 0, 5, 5
)
prec_sim <- c(
0, 0.2, 0.1, 0, 0, 3, 1, 1, 1, 1, 0, 3,
0, 10, 4, 1, 0.3, 0.5, 0.5, 0.5, 0.5, 0, 0.25, 0.25,
0.25, 0, 0.5, 3, 0, 5, 0, 0, 0, 0, 0.5, 0,
0.25, 0.2, 0, 0.2, 0, 0, 0, 0, 1, 2, 1, 0
)- Escreva o código para calcular as estatísticas abaixo, entre os vetores de valores observados (
obs) e previstos (prev) por um dado modelo atmosférico, em um dado local.
- O Viés relativo (%)27.
\[PBIAS = 100\frac{\sum_{i=1}^{n}(Prev_{i}-Obs_{i})}{\sum_{i=1}^{n}(Obs_{i})}\].
- Coeficente de eficiência de Nash-Sutcliffe (NSE)28.
\[NSE = 1 - \frac{\sum_{i=1}^{n} (Obs_{i}-Sim_{i})^{2}}{\sum_{i = 1}^{n} (Obs_{i}-\bar{Obs}_{i})^{2}}\]
v_obs <- c(
-0.49, 0.27, -0.48, 0.8, -1, 0.1, -1.16,
0.58, -1.6, -0.31, 0.45, -0.98, 0.19, 0.73,
-0.49, -0.04, -0.11, 0.46, 2.02, -1.05
)
v_prev <- c(
NA, -0.49, 0.27, -0.48, 0.8, -1, 0.1, -1.16,
0.58, -1.6, -0.31, 0.45, -0.98, 0.19, 0.73,
-0.49, -0.04, -0.11, 0.46, 2.02
)Mede a tendência média dos valores previstos (ou simulados) em serem maiores (superestimativa) ou menores (subestiva) que os observados. O valor ótimo é 0, menores valores indicam melhor desempenho. Valores positivos indicam tendência de superestimativa e negativos de subestimativa.↩
NSE é uma estatística normalizada que que determina a magnitude relativa da variância residual (ruído) comparada a variância dos dados medidos (informação). NSE varia de -Inf a 1. Essencialmente, quanto mais próximo a 1, melhor o modelo.↩