A.3 Operações matriciais
A.3.1 Multiplicação matricial
Operações algébricas, incluindo a multiplicação *, atuam elemento a elemento sobre matrizes. Mas se a intenção é fazer uma multiplicação matricial (Figura A.1) usamos o operador (%*%).
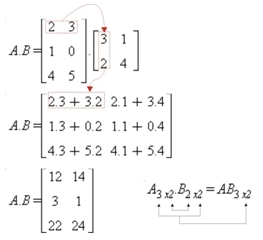
Figure A.1: Multiplicação matricial.
# multiplicação de duas matrizes
A <- matrix(c(2, 1, 4, 3, 0, 5), ncol = 2)
A
#> [,1] [,2]
#> [1,] 2 3
#> [2,] 1 0
#> [3,] 4 5
B <- matrix(c(3, 2, 1, 4), ncol = 2)
B
#> [,1] [,2]
#> [1,] 3 1
#> [2,] 2 4
A * B # erro pela diferença nas dims entre as matrizes
#> Error in A * B: non-conformable arrays
prod_mat <- A %*% B
prod_mat
#> [,1] [,2]
#> [1,] 12 14
#> [2,] 3 1
#> [3,] 22 24
# multiplicação de uma matriz por um escalar
m <- matrix(1:16, nrow = 4, byrow = TRUE)
m
#> [,1] [,2] [,3] [,4]
#> [1,] 1 2 3 4
#> [2,] 5 6 7 8
#> [3,] 9 10 11 12
#> [4,] 13 14 15 16
m * 2
#> [,1] [,2] [,3] [,4]
#> [1,] 2 4 6 8
#> [2,] 10 12 14 16
#> [3,] 18 20 22 24
#> [4,] 26 28 30 32A.3.2 Adição matricial
m
#> [,1] [,2] [,3] [,4]
#> [1,] 1 2 3 4
#> [2,] 5 6 7 8
#> [3,] 9 10 11 12
#> [4,] 13 14 15 16
m + m
#> [,1] [,2] [,3] [,4]
#> [1,] 2 4 6 8
#> [2,] 10 12 14 16
#> [3,] 18 20 22 24
#> [4,] 26 28 30 32A.3.3 Produto escalar
u <- 1:3
v <- c(5, 12, 13)
u * v
#> [1] 5 24 39
# produto escalar = u.v = 1*5 + 2*12 + 3*13
crossprod(u, v)
#> [,1]
#> [1,] 68A.3.4 Determinante
# matriz exemplo
mat_ex <- matrix(c(1, -7, 3, 5, -9, 2, 6, 6, 1), ncol = 3)
det(mat_ex)
#> [1] 182A.3.5 Solução de sistemas lineares
\[ \left\{\begin{matrix} x_1 + x_2 = 2 \\ -x_1 + x_2 = 4 \end{matrix}\right. \]
Qual os valores de \(x_1\) e \(x_2\)?
# matrizes do sistema linear
coefs <- matrix(c(1, -1, 1, 1), ncol = 2)
y <- c(2, 4)
x <- solve(coefs, y)
x
#> [1] -1 3A.3.6 Produto cartesiano
O produto cartesiano de dois conjuntos A e B é representado por \(A \times B\). O resultado é o conjunto de todos pares ordenados (a, b) tal que \(a \belong b\).