7.6 Exercícios
- Crie um vetor com os valores de \(e^{x}cos{x}\) para os valores de \(x = (3, 3.1, 3.2, ..., 6\)).
- Crie os seguintes vetores.
\((0.1^{3}\times0.2^{1}, 0.1^{6}\times0.2^{4}, ..., 0.1^{36}\times0.2^{34})\)
\((2, \frac{2^{2}}{2}, \frac{2^{3}}{3}, ..., \frac{2^{25}}{25})\)
- Reproduza a criação do vetor dias da semana (
dds) mostrado abaixo.
Domingo Segunda-feira Terca-feira Quarta-feira Quinta-feira
1 2 3 4 5
Sexta-feira Sabado
6 7 - Escreva os códigos necessários para determinar:
o vetor lógico indicando quais números são pares na sequência de valores 19, 70, 57, 17, 91, 90, 13, 78, 44, 51. Calcule o total de números ímpares.
Se um ano é bissexto. Verifique os resultados de seu código para os anos 1913, 1977, 1961, 1910, 2005, 2004, 1905, 1989, 1945, 1954. Calcule o total de anos com 365 dias.
- Quais códigos para gerar os seguintes dados:
[1] -20 0 10 20 30 40[1] -1.00 -0.75 -0.50 -0.25 0.00 0.25 0.50 0.75 1.00 [1] -3.141593 -2.570394 -1.999195 -1.427997 -0.856798 -0.285599 0.285599
[8] 0.856798 1.427997 1.999195 2.570394 3.141593 [1] 1 1 1 1 1 2 2 2 2 3 3 3 4 4 5 [1] 1 1 1 1 1 2 2 2 2 3 3 3 4 4 5 4 4 3 3 3 2 2 2 2 1 1 1 1 1- Dica: lembre da função
rep()e seus argumentoseachetimes. Experimente usar vetores nesses argumentos.
[,1] [,2] [,3] [,4]
[1,] 1 1 2 2
[2,] 1 1 2 2
[3,] 3 3 4 4
[4,] 3 3 4 4- Como a partir da matriz gerada na letra f você pode obter a matriz abaixo?
[,1] [,2] [,3] [,4]
[1,] 1 1 3 3
[2,] 1 1 3 3
[3,] 2 2 4 4
[4,] 2 2 4 4- Qual o código para converter a matriz gerada na letra g no vetor abaixo?
[1] 1 1 3 3 1 1 3 3 2 2 4 4 2 2 4 4- Como obter as seguintes sequências a partir dos vetores fornecidos usando a mesma solução para todos casos?
- v3 = (10, 0.5, 8, 4)
[1] 1 2 3 4- v2 = (10, 0.5)
[1] 1 2- v1 = (10)
[1] 1- v0 = ()
integer(0)- Calcule a soma cumulativa dos números 2, 3, 4, 5, 6. Dica: ver a função
cumsum(). (b) Calcule a soma cumulativa destes números mas na ordem reversa. Dica: ver a funçãorev().
- Calcule a soma cumulativa dos números 2, 3, 4, 5, 6. Dica: ver a função
- Os dados abaixo são de precipitação horária de um evento severo ocorrido em 03/12/2012 em Santa Maria-RS.
| hora | prec |
|---|---|
| 9 | 0.0 |
| 10 | 0.0 |
| 11 | 0.0 |
| 12 | 0.0 |
| 13 | 0.0 |
| 14 | 0.0 |
| 15 | 0.0 |
| 16 | 21.4 |
| 17 | 41.2 |
| 18 | 2.6 |
| 19 | 1.0 |
| 20 | 0.4 |
| 21 | 0.0 |
Como seria o código para determinar a soma cumulativa da precipitação horária? Salve seu resultado em um vetor chamado
prec_acum. Interprete o resultadoc(NA, diff(prec_acum)).Mostre o código para encontrar o horário de ocorrência da precipitação máxima?
Mostre o código para obter a hora de início e fim do evento de precipitação severa. Qual foi a duração do evento?
Qual foi a precipitação total do evento? Quanto da precipitação total do evento, em %, ocorreu até às 17 h?
- EXERCÍCIO RESOLVIDO. Considere o vetor
xdefinido pelos números descritos abaixo. Mostre como encontrar o primeiro número positivo localizado após o último número negativo. Por exemplo, seja o vetorzdefinido pelos valores (11, 10, 15, 2, 6, -15, -10, -22, -8, 5, 7, 2, 12, 8, 4, 1, 3, -3, -1, 30, 14). Os valores selecionados seriam 5 e 30.
Um possível código para chegar a esse resultado seria:
x <- c(
11, 10, 15, 2, 6, -15, -10, -22, -8, 5,
7, 2, 12, 8, 4, 1, 3, -3, -1, 30, 14
)
# x1 <- ifelse(x > 0, 1, 0)
# cópia de x
x01 <- x
# substituo x positivo por 1 e x negativo por 0
x01[x > 0] <- 1
x01[!x > 0] <- 0
res <- x[which(diff(x01) == 1) + 1]
res
#> [1] 5 30- Mostre o código para resolver as seguintes tarefas. Considere o vetor
preccom valores de precipitação diária indicado abaixo.
prec <- c(
0, 0, 0, 0.8, 0, 0.01, 0.75, 0,
0, 0, 0, 0.35, 0.08, 0, 0, 0, 0, 0.31, 0, 3.57, 12.17, 0, 0,
0, 0.04, 3.16, 0, 0.95, 0.79, 0, 0, 0, 0, 0, 3.51, 0, 0, 0.16,
0, 0, 8.16, 0.54, 4.39, 1.24, 0, 0, 0, 0, 0, 2.43, 0, 0, 0, 0,
0, 7.18, 0, 0, 0.26, 0, 0, 0.28, 0, 0, 0.09, 0.38, 0, 0, 0, 0,
0, 0, 0.51, 0, 0, 0, 0, 0, 0, 0.67, 0, 0, 0, 0, 0.15, 0, 0.82,
0, 0, 0, 0, 0, 0, 0, 0, 0.37, 0, 0.58, 4.95, 0, 0, 0, 0, 0, 7.68,
0, 0, 0.37, 0, 1.56, 0, 0, 0, 0.34, 0.48, 0, 4.21, 2.28, 4.3,
0, 3.38, 0, 0, 0, 0, 7.28, 0, 4.89, 3.91, 0, 0, 0, 0, 0, 0, 2.93,
0, 2.49, 0.77, 0, 2.9, 3.53, 0.83, 0, 0, 0, 0.94, 0.59, 0, 0,
0, 0, 0.04, 0, 0.65, 0, 0, 0, 6.23, 0.09, 0, 0.66, 0, 0, 0, 4.42,
0, 0, 0, 0.84, 0, 0, 0, 0, 0, 0.09, 0, 0, 0.08, 0, 0.66, 0, 0,
0, 0.06, 0, 0, 0, 3.28, 0, 0.8, 5.69, 0.8, 0
)Quantos dias ocorreram no intervalo 0 < prec < 0.25?
Substitua os valores de chuva registrados no intervalo 0 < prec < 0.25 por 0.
Crie um vetor denominado
prec01indicando o estado da precipitação (chuvoso = 1, seco = 0) baseado no limiar de 0.25 mm para detecção de chuva pelo pluviômetro.Qual a probabilidade de chuva dessa série de precipitação diária?
Qual a probabilidade de chover dois dias consecutivos (
p11)? Calcule a probabilidade de chover em qualquer um de dois dias consecutivos (p01 + p10)?Determine a duração de cada evento chuvoso (número de dias consecutivos).
Dica: comece encontrando a posição do início do evento e depois a posição final do envento. A diferença entre as posições fornece a duração do evento. O exercício resolvido (9) é análogo a esse exercício.
O resultado esperado é um vetor que identifique o evento e sua duração.
duracao
#> evento1 evento2 evento3 evento4 evento5 evento6 evento7 evento8
#> 1 1 1 1 2 1 2 1
#> evento9 evento10 evento11 evento12 evento13 evento14 evento15 evento16
#> 4 1 1 1 1 1 1 1
#> evento17 evento18 evento19 evento20 evento21 evento22 evento23 evento24
#> 1 1 2 1 1 1 2 3
#> evento25 evento26 evento27 evento28 evento29 evento30 evento31 evento32
#> 1 1 2 1 2 3 2 1
#> evento33 evento34 evento35 evento36 evento37 evento38 evento39
#> 1 1 1 1 1 1 3- EXERCÍCIO RESOLVIDO. Dado o vetor
tempmostrado abaixo.
temp <- c(
NA, NA, 27L, 7L, 4L, 0L, 26L, 15L, 25L, NA, NA, NA, NA, 6L,
29L, 18L, 17L, 23L, 20L, 1L, 30L, 13L, NA, NA, NA, NA, NA, NA,
NA, 19L
)- Como você pode codificar a obtenção de um vetor com zeros nos valores válidos e com números sequenciais dentro das falhas?
# vetor lógico de falhas
eh_falha <- is.na(temp)
# soma cumulativa de falhas
acum_falhas <- cumsum(eh_falha)
# calculando soma a partir do início da falha
seq_falhas <- acum_falhas - cummax((!eh_falha) * acum_falhas)
seq_falhas
#> [1] 1 2 0 0 0 0 0 0 0 1 2 3 4 0 0 0 0 0 0 0 0 0 1 2 3 4 5 6 7 0- Como a partir do vetor resultante em 11.b obter um vetor cujo os valores dentro das falhas indique a ordem de ocorrência da falha.
(ordem_falhas <- cumsum(seq_falhas == 1) * as.integer(eh_falha > 0))
#> [1] 1 1 0 0 0 0 0 0 0 2 2 2 2 0 0 0 0 0 0 0 0 0 3 3 3 3 3 3 3 0- Qual o tamanho de cada falha.
pos_fim_falha <- which(c(NA, diff(ordem_falhas)) < 0) - 1
(tamanho_falhas <- seq_falhas[pos_fim_falha])
#> [1] 2 4 7
# names(tamanho_falhas) <- paste0("falha", unique(ordem_falhas[ordem_falhas > 0]))
names(tamanho_falhas) <- paste0("falha", seq_along(tamanho_falhas))
tamanho_falhas
#> falha1 falha2 falha3
#> 2 4 7- Determine o tamanho da maior falha?
(max_falha <- max(tamanho_falhas))
#> [1] 7- Para os valores de velocidade (\(V_h\)) e a direção do vento (\(\theta\)) (na convenção meteorológica):
\(V_h\) = (10, 10, 10, 10, 14.142, 14.142, 14.142, 14.142, 0)
\(\theta\) = (270, 180, 360, 90, 225, 315, 135, 45, 0)
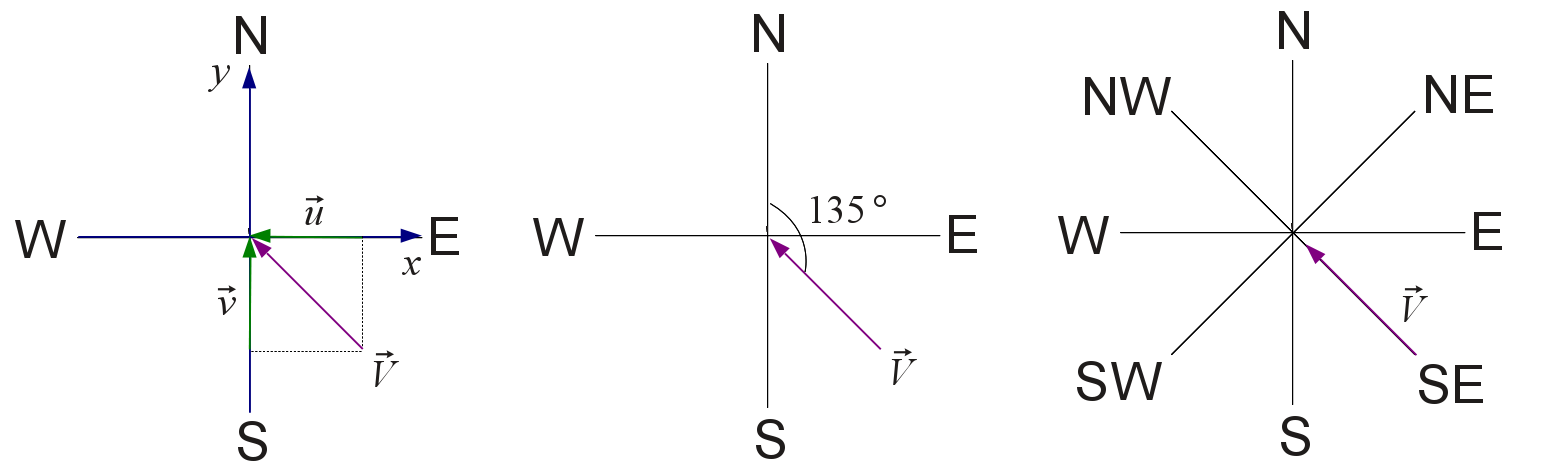
- Determine as componentes zonal e meridional do vento.
\[u = -V_{h} \cdot sin(\theta_{rad})\] \[v = -V_{h} \cdot cos(\theta_{rad})\]
- Faça os cálculos necessários para reconstruir \(V_h\) e \(\theta\) a partir de \(u\) e \(v\) determinados no item a. Por convenção, a direção do vento \(\theta\) em condições calmas (\(V_h\) < 0.5 m s-1) é assumida como 0°.
\[V_{h} = \sqrt{(u^2 + v^2)}\] \[\theta_{mat} = {\rm atan2}(-u, -v)\cdot\frac{180}{\pi}\] \[ \theta = \left\{\begin{matrix} \theta_{mat} + 360 & se & \theta_{mat} < 0 \\ 0 & se & u = 0,\: v = 0 \: \: ou \: \: V_{h} < 0.5\\ \end{matrix}\right. \]
Como resultado monte um dataframe com todas variáveis derivadas.
| u | v | ws | wd | wd_uv | dir |
|---|---|---|---|---|---|
| 10 | 0 | 10.000 | 270 | 270 | Oeste |
| 0 | 10 | 10.000 | 180 | 180 | Sul |
| 0 | -10 | 10.000 | 360 | 360 | Norte |
| -10 | 0 | 10.000 | 90 | 90 | Leste |
| 10 | 10 | 14.142 | 225 | 225 | Sudoeste |
| 10 | -10 | 14.142 | 315 | 315 | Noroeste |
| -10 | 10 | 14.142 | 135 | 135 | Sudeste |
| -10 | -10 | 14.142 | 45 | 45 | Nordeste |
| 0 | 0 | 0.000 | 0 | 0 | Calmo |
Dica: ver figura abaixo.
- Para as séries de
prec_obseprec_simcalcule:
- a proporção corretamente prevista \(PC = \frac{wc+dc}{n}\)
- o índice de sucesso crítico \(CSI=\frac{wc}{wc+wi+di}\).
Onde \(wc\) e \(dc\) são as previsões corretas de dias úmidos (\(prec > 0.25\) mm dia-1) e secos respectivamente, \(wi\) e \(di\) são as previsões incorretas de dias úmidos e secos respectivamente. \(n\) é o n° total de previsões.
prec_obs <- c(
0, 0, 0, 0.5, 1, 6, 9, 0.2, 1, 0, 0, 0.25,
10, 15, 8, 3, 0, 0, 0, 0, 0, 0, 0.25, 0,
0, 0, 1, 5, 0, 20, 0, 0, 0, 0, 1, 1,
0, 2, 12, 1, 0, 0, 0, 0, 0, 0, 5, 5
)
prec_sim <- c(
0, 0.2, 0.1, 0, 0, 3, 1, 1, 1, 1, 0, 3,
0, 10, 4, 1, 0.3, 0.5, 0.5, 0.5, 0.5, 0, 0.25, 0.25,
0.25, 0, 0.5, 3, 0, 5, 0, 0, 0, 0, 0.5, 0,
0.25, 0.2, 0, 0.2, 0, 0, 0, 0, 1, 2, 1, 0
)- Escreva o código para calcular o coeficiente de correlação de Pearson (
r) entre os vetoresobseprev.
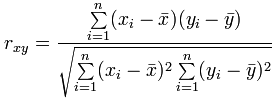
Confira seu resultado com a saída da função cor(obs, prev).
obs <- c(
-0.49, 0.27, -0.48, 0.8, -1, 0.1, -1.16,
0.58, -1.6, -0.31, 0.45, -0.98, 0.19, 0.73,
-0.49, -0.04, -0.11, 0.46, 2.02, -1.05
)
prev <- c(
NA, -0.49, 0.27, -0.48, 0.8, -1, 0.1, -1.16,
0.58, -1.6, -0.31, 0.45, -0.98, 0.19, 0.73,
-0.49, -0.04, -0.11, 0.46, 2.02
)- Construa uma função para converter valores de temperatura em K para °C e outra para converter ângulos de radianos para graus. Utilize dois exemplos para mostrar que suas funções funcionam corretamente.