2.4 Balanço Hídrico
O ponto inicial da maioria das análises hidrometoerológicas envolvem a aplicação do balanço de massa. A equação do balanço de massa para um dado sistema pode ser derivada a partir do teorema do Transporte de Reynolds (MAYS, 2005).
O teorema inicia com a definição de um volume de controle no espaço, definido por uma superfície de controle (Figura 2.9).
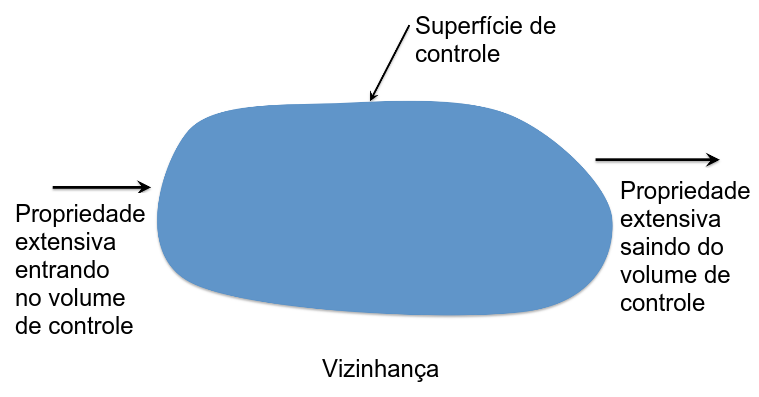
Figura 2.9: Esquema básico de um volume de controle com fluxos através da superfície de controle.
Propriedades de um fluído podem ser extensivas ou intensivas. As extensivas são aquelas relacionadas de alguma forma à massa total do sistema, incluindo a massa (\(m\)), momentum (\(m \vec{V}\)) e energia (\(E\)). Propriedades intensivas são aquelas geralmente normalizadas pela massa (ex.: momentum por unidade de massa, ou seja, velocidade; energia por unidade de massa, etc). Uma propriedade extensiva pode ser representada por \(\mathbf{B}\) e um intensiva como \(B\) (\(\frac{d\mathbf{B}}{dt}\)). A equação geral para o volume de controle pode ser expressa como (MAYS, 2005):
\[\begin{equation} \frac{d\mathbf{B}}{dt} = \frac{d}{dt}\int_{VC} \rho\;B\;dV +\int_{CS}\rho\;B\mathbf{V}\cdot d\mathbf{A} \tag{2.1} \end{equation}\]
onde os termos individuais são:
\(\frac{d\mathbf{B}}{dt} \equiv\) taxa total de variação da propriedade extensiva
\(\frac{d}{dt}\int_{VC} \rho\;B\;dV \equiv\) taxa de variação da propriedade extensiva no volume de controle (onde \(\rho\) é a densidade do fluido e \(dV\) é um volume diferencial)
\(\int_{CS}\rho\;B\mathbf{V}\cdot d\mathbf{A}\) taxa liquida do fluxo através da superfície de controle (onde \(\mathbf{V}\) é a velocidade e \(dA\) é a área diferencial da superfície do controle)
A equação do balanço de massa (ou continuidade) é derivada do teorema do transporte de Reynolds definindo \(\mathbf{B}\) como massa (fazendo \(B = 1\)) e portanto o termo do lado esquerdo da equação é igual a zero, o que leva a:
\[\begin{equation} \frac{d}{dt}\int_{VC} \rho\;dV = \frac{dM}{dt}= -\int_{SC}\rho\mathbf{V}\:d\mathbf{A} \tag{2.2} \end{equation}\]
a qual expressa que a taxa de variação do armazenamento de massa no volume de controle (massa/tempo) é balanceado pela taxa líquida do fluxo de massa através da superfície de controle. Diversas suposições podem simplificar a equação (2.2), incluindo densidade constante (apropriada no caso do escoamento de água líquida e problemas de armazenamento), nesse caso:
\[\begin{equation} \frac{d}{dt}\int_{VC} dV = -\int_{SC}\mathbf{V}\cdot d\mathbf{A} \tag{2.3} \end{equation}\]
a qual pode ser simplesmente escrita como:
\[\begin{equation} \frac{dS}{dt} = \sum_{i}{I_{i}} - \sum_{i}{O_{i}} \tag{2.4} \end{equation}\]
onde \(S\) é o volume de armazenamento e o lado direito é o soma das entradas (\(I_i\)) menos a soma das saída (\(O_i\)) em termos de fluxo volumétrico através da superfície do volume de controle. Um ponto-chave é que apenas fluxos através do superfície de controle precisam ser considerada no balanço de massa equação. Fluxos internos não contribuem para mudanças no armazenamento de massa/volume. Este fato é frequentemente usado na construção de um volume de controle para eliminar fluxos que são desconhecidos tornando-os fluxos internos. Portanto, para aplicar a equação adequadamente, um volume de controle deve ser definido explicitamente. Outro simplificação bastante usada é a de estado estacionário, situação em que o termo de armazenamento é igual a zero, produzindo:
\[\begin{equation} \sum_{i}{I_{i}} = \sum_{i}{O_{i}} \tag{2.5} \end{equation}\]
No contexto de aplicações do balanço massa (ou outras), várias formas de fluxos são usadase é importante diferenciá-los, assim como suas unidades. Fluxos de massa (ou seja, usadosna equação (2.1)) têm unidades de massa/tempo (por exemplo, kg s-1). Fluxos volumétricos (ou seja, usadosna Equação (2.5) têm unidades de volume/tempo (por exemplo, m3 s-1). Para converter entre os dois, a densidade do fluido pode ser usada, ou seja, para água:
\[\frac{kg}{s} \times \frac{1}{\rho} = \frac{m^{3}}{s}; \rho = 1000\: kg\: m^{-3}\]
Muitas vezes, a densidade de fluxo é usada no lugar do fluxo, que é simplesmente, ou o fluxo de massa ou volumétrico, normalizado pela área da seção transversal apropriada, através da qual o fluxo está ocorrendo, ou seja
\[Massa: \frac{kg}{s} \times \frac{1}{A} \rightarrow \frac{kg}{m^{2}s}\]
\[Volume: \frac{m^{3}}{s} \times \frac{1}{A} \rightarrow \frac{m}{s} ou \left ( \frac{mm}{dia}, \: \frac{m}{ano} \right )\]
onde, como mostrado acima, se a densidade do fluxo de massa for conhecida, a densidade de fluxo volumétrico pode ser obtida dividindo-se pela densidade da água. A densidade de fluxo volumétrica é uma forma comum de expressar fluxos em hidrometeorologia. Por exemplo, a precipitação média anual em Santa Maria é 1100 mm ano-1, que está implícito ocorrer sobre uma determinada área. Para obter o fluxo volumétrico real seria necessário multiplicar pela área da superfície de Santa Maria-RS, sobre a qual a densidade de fluxo ocorre.
Como será discutido em mais detalhes posteriormente, os fluxos de água e energia são diretamente relacionados. O exemplo mais relevante é que o fluxo de evaporação está diretamente ligado ao fluxo de calor associado a mudança de fase. Por exemplo, o fluxo de calor latente, associado à mudança de fase é simplesmente a densidade de fluxo de massa multiplicada pelo calor latente de vaporização:
\[Fluxo\: de\: energia = \lambda_{v} \times Fluxo\: de\: massa; \lambda_{v} = 2,5 \times 10^6\: J\: kg^{-1}\]
onde as unidades de W m-2 são as mais comumente usadas para fluxos de energia (na verdade, densidades de fluxo) em hidrometeorologia.
2.4.1 Balanço Hídrico Global
Para termos uma melhor noção dasescalas de tempo dos fluxos hidrológicos e do balanço de massa, é instrutivo começar na escala global. Se considerarmos um volume de controle cobrindo toda a superfície do globo (Figura 2.10), os fluxos relevantes através da superfície de controle são a precipitação e a evapotranspiração no continente e no oceano. Note que o escoamento entre o continente e o oceano é um fluxo interno e, portanto, não é relevante para o balanço de massa do volume de controle que escolhemos (retângulo vermelho). O balanço global instantâneo de massa (ou de volume) pode então ser escrito como:
\[\begin{equation} \frac{dS}{dt} = P_{con} - ET_{con} + P_{oce} - ET_{oce} \tag{2.6} \end{equation}\]
onde S representa a massa ou volume armazenado nos reservatórios de água do oceano e continente com unidades consistentes (em termos de massa ou volume). Dada a equação acima, se todos os fluxos instantâneos forem conhecidos, então a variação do armazenamento pode ser determinada. Alternativamente, se a variação de armazenamento for conhecida e todos os fluxos, exceto um, forem conhecidos, a equação pode ser usada para resolver o fluxo desconhecido como resíduo da Equação (2.6).
Na prática, os termos do balanço de massa instantâneo são difíceis, senão impossíveis, de se estimar com precisão (especialmente em grandes escalas). Portanto, para simplificar a análise hidrológica, muitas vezes usamos a média de longo prazo da equação de balanço de massa acima, onde podemos usar o operador de média de tempo:
\[\begin{equation} \bar{X} = \frac{1}{T}\int_{t}^{t+T} X \, dt \tag{2.7} \end{equation}\]
onde T é um intervalo temporal e a equação acima pode ser aplicada a cada termo na equação de balanço de massa:
\[\begin{equation} \bar{\frac{dS}{dt}} = \bar{P}_{con} - \bar{ET}_{con} + \bar{P}_{oce} - \bar{ET}_{oce} \tag{2.8} \end{equation}\]
A questão então é: se o período de média for longo o suficiente, podemos dizer algo sobre qualquer um desses termos? No longo prazo, podemos dizer razoavelmente que a variação (média) do armazenamento deve ser próxima de zero ou pelo menos muito menor do que os fluxos médios. Isso implicitamente assume alguma estacionariedade no sistema (ou seja, é um estado estacionário no longo prazo). Em geral, quanto mais longo for o período da média, mais precisa será a suposição. No mínimo um ano deve ser usado para Obter a média ao longo do ciclo sazonal (ou seja, a maioria das regiões tem uma estação chuvosa onde o armazenamento de água aumenta e uma estação seca onde ele dimuninui). Qualquer período menor seria considerado uma violação da suposição de estado estacionário.
Tirando a média de longo prazo resulta em:
\[\begin{equation} \bar{\frac{dS}{dt}} \approx 0 = \bar{P}_{con} - \bar{ET}_{con} + \bar{P}_{oce} - \bar{ET}_{oce} = \bar{P}_{glob} - \bar{ET}_{glob} \tag{2.9} \end{equation}\]
\[\begin{equation} \rightarrow \bar{P}_{glob} = \bar{ET}_{glob} \tag{2.10} \end{equation}\]
o que deveria fazer sentido porque, se esses fluxos não estivessem em equilíbrio, a água estaria se acumulando a longo prazo na atmosfera (se a evapotranspiração excedesse a precipitação) ou no continente/oceano (se a precipitação excedesse a evapotranspiração). A partir dos dados, estima-se que:
\[\bar{P}_{glob} = \bar{ET}_{glob} \approx 953\: mm\: ano^{-1}\]
onde esse valor está expresso em termos de uma densidade de fluxo volumétrico (ou seja, normalizado pela superfície da Terra). Em fluxo volumétrico, seria igual a 1332 km3 dia-1. Podemos pensar neste fluxo como a taxa média global do ciclo hidrológico. Em outras palavras, esta é a quantidade média de água que se move através dos vários reservatórios hidrológicos. Observe que os fluxos instantâneos em qualquer ponto e tempo podem ser muito diferente (como será discutido mais tarde).
Um conceito útil envolvendo o tamanho dos reservatórios e os fluxos entre eles é o Tempo de Residência \(T_{r}\). O \(T_{r}\) [T] é uma medida de quanto tempo, em mmédia, uma molécula de água gasta dentro reservatório antes de mover-se para outro reservatório do Ciclo Hidrológico. O \(T_{r}\) é facilmente calculado para sistemas estacionários, ou seja quando o fluxo de entrada e saída são idênticos:
\[T_{r} = \frac{V}{F} \; \left [ \frac{L^{3}}{L^{3}.T^{-1}} \right ]\]
O \(T_{r}\) fornece um indicação do tempo necessário para substituir toda água do reservatório. A água nos oceanos tem um tempo de residência de \(\approx\) 2600 anos, enquanto o da água dos rios, lagos e áreas úmidas é de \(\approx\) 134 dias. O \(T_{r}\) água na atmosfera é de somente \(\approx\) 10 dias, ou seja, um dos reservatórios mais dinâmicos do ciclo hidrológico e contribui muito para a variabilidade do sistema.
A determinação do \(T_{r}\) dos oceanos é complicada pelo fato há uma camada relativamente rasa (da ordem de 100 m de profundidade) que interage prontamente com os reservatórios atmosfericos e terrestres, mas esta camada está sobre uma camada muito mais profunda e isolada de água salina que move-se lentamente.Dada esta taxa, podemos estimar o tempo médio de residência nos vários reservatórios. Com as estimativas dos volumes dos reservatórios (Tabela 2.1), os tempos de residência podem ser estimados e são mostrados na Tabela 2.2.
| Reservatório | Volume (Km3) | Tempo de residência | unidade |
|---|---|---|---|
| Oceano | 1.335.040.000 | 2.746 | anos |
| Áreas congeladas | 26.372.000 | NA | anos |
| Água subterrânea | 15.300.000 | 31 | anos |
| Lagos, Rios e áreas úmidas | 178.000 | 134 | dias |
| Água no solo | 122.000 | 92 | dias |
| Atmosfera | 12.700 | 10 | dias |
É muito importante ter em mente que os números acima são médias globais de longo prazo. Variabilidade significativa existe na maioria dos fluxos hidrológicos, tanto no espaço quanto no tempo.
Na verdade, é justamente essa variabilidade que deve ser acomodada por projetos de sistemas hídricos. Alguns exemplos interessantes para ilustrar a variabilidade espacial, incluem os lugares mais secos e mais úmidos da Terra. Para ilustração, podemos comparar a precipitação média de longo prazo como uma medida representativa da hidrologia local. Por exemplo, Los Angeles recebe uma média de 380 mm ano-1, tornando-a um local relativamente seco. No entanto, o lugar mais seco da Terra é o Deserto do Atacama, no Chile. Em partes do Atacama nunca houve foi registrado chuva, e sobre todo o deserto, a média das chuvas é menos de 1 mm ano-1! A falta de água contribui para um paisagem particularmente rígida com pouca ou nenhuma vida, ao ponto que muitas vezes é comparada à superfície de Marte.
Em contraste, o lugar “mais úmido” da Terra é geralmente considerado Cherrapunji, Índia, que recebe uma precipitação média anual de 11100 mm ano-1. Além disso, devido ao clima de monções, a maior parte dessa chuva ocorre na estação chuvosa que dura de 3 a 6 meses. Tendo em mente que esta é a média de longo prazo, outro exemplo interessante é a precipitação máxima anual observada em Cherrapunji, que foi de 26500 mm! Esses dois exemplos fornecem extremidades interessantes do espectro hidrológico, onde em um a água é extremamente escassa, tornando o abastecimento hídrico um problema crítico. No outro, o excesso de água causa problemas extremos de inundação. Além desses dois exemplos de extrema variabilidade espacial hidrológica, é importante ter em mente a variabilidade temporal. Por exemplo, a maior parte dos 380 mm anuais de precipitação em Los Angeles ocorre no inverno (dezembro-março), que contrasta com Cherrapunji, que recebe quase toda chuva durante o verão. Ao fazer qualquer análise hidrológica, é importante definir claramente as escalas espaciais e temporais relevantes de interesse.
2.4.2 Análise quantitativa dos fluxos hidrológicos globais
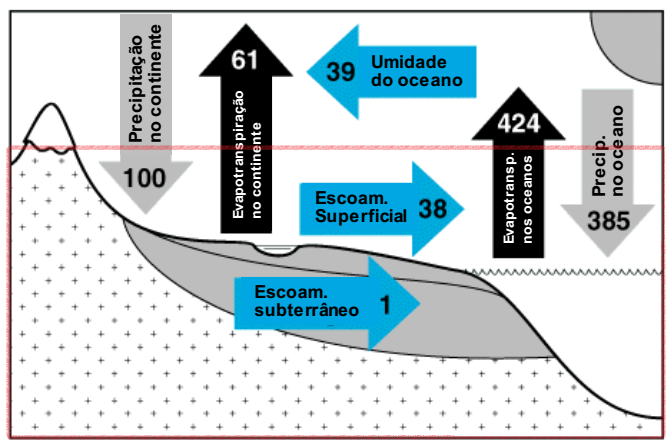
Figura 2.10: Principais fluxos do ciclo hidrológico global. Os valores estão expressos em unidades relativas à Precipitação média anual nos continentes (100 u.r. = 119.000 km3). Setas pretas indicam fluxos para a atmosfera, setas cinzas indicar setas para o oceano ou continente e setas azuis idicam fluxos laterais. Adaptado de Maidment (1993).
Anualmente, \(\approx\) 577150 km3 ano-1 de água (o que equivale5 a 1132 mm), deixam a atmosfera na forma de Precipitação. A mesma quantidade retorna para atmosfera anualmente como Evaporação, por isso a quantidade de água na atmosfera não muda com o tempo e o ciclo hidrológico na escala global é fechado.
A água não é uniformemente distribuída entre os continentes e o oceano. A Precipitação média nos continente é 119000 km3 (cerca de 21% da Precipitação média global. Tomando este valor como unidade relativa (u.r) para os demais fluxos do balanço hídrico global (100 u.r = 119.000 km3), 61% desta precipitação (487 mm) evapora de volta para atmosfera.
Nos oceanos a evaporação supera a precipitação, resultando em uma diferença de -39 u.r. Este excedente de evaporação dos oceanos (\(\approx\) 9%) é transportado pelo vento para os continente e contribui para precipitação nos continentes6. No continente a precipitação excede a evapotranspiração gerando um excesso (39 u.r, ou 312 mm) que escoa em grande parte pela superfície e o subsolo para o oceano, reestabelecendo a maior perda de água por evaporação no oceano.
O runnof total estimado é equivalente a 39% da precipitação continental, portanto um coeficiente de escoamento de 0,39. Esta quantidade representa o que é chamado convencionalmente de recursos hídricos renováveis. Mas nem toda esta quantidade é acessível para uso humano, porque parte da água escoa para rios remotos e parte da água das enchentes sazonais não podem ser capturadas antes de atingir os oceanos. De acordo com a FAO (2003), 9.000-14.000 km3 (20-31% dos recursos hídricos renováveis) é o total de água economicamente disponível para o uso humano.
2.4.3 Balanço Hídrico Atmosférico
2.4.3.1 Água precipitável
Figura 2.11.
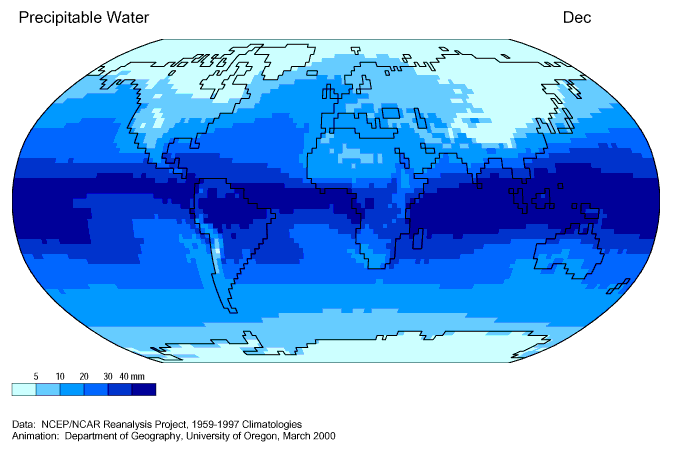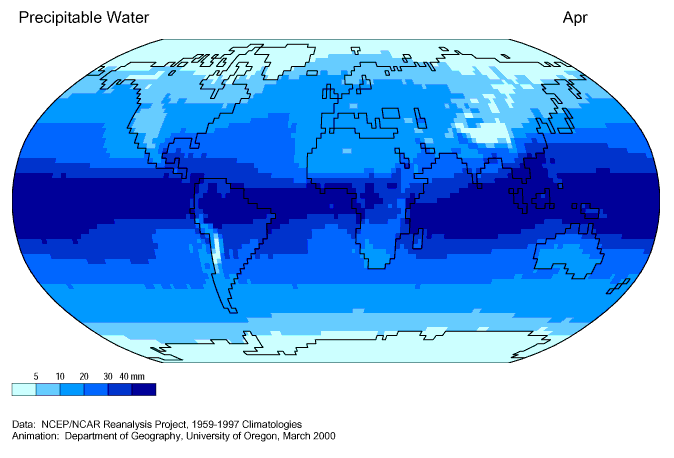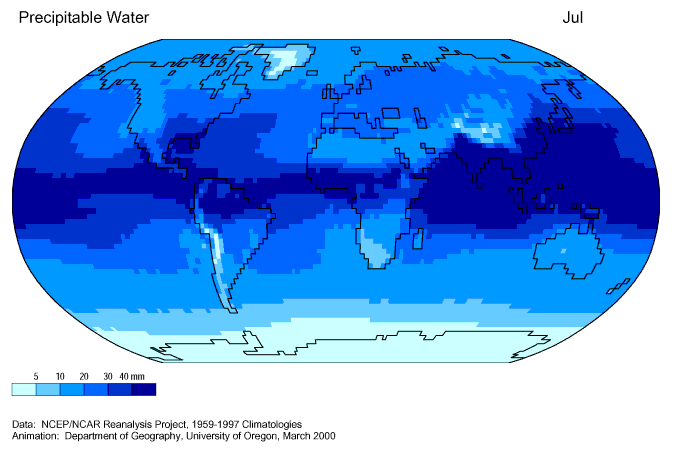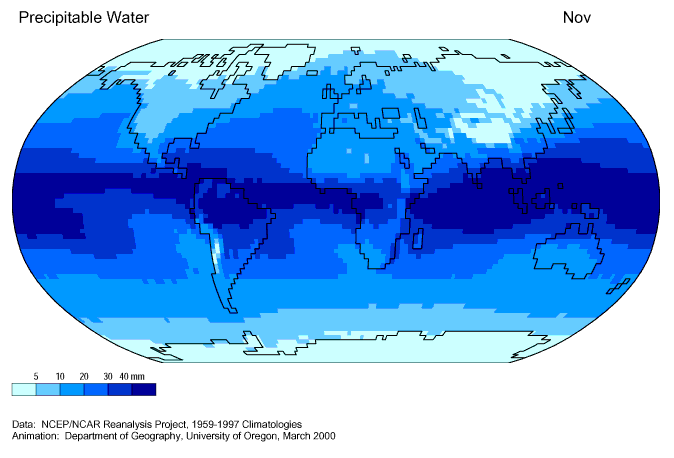
Figura 2.11: Climatologia da água precipitável. Fonte: climvis
Divergência horizontal do fluxo de vapor d’água integrado na vertical.
Figura 2.12.
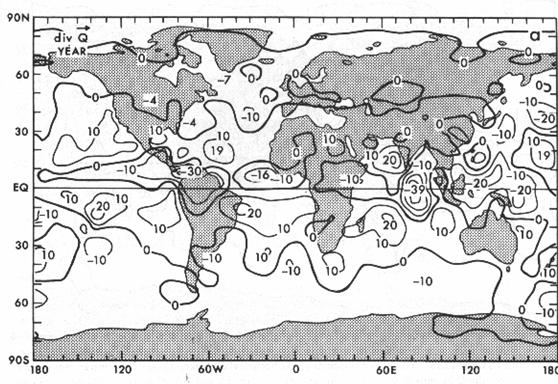
Figura 2.12: Climatologia anual da Divergência horizontal do transporte de vapor d’água integrado na atmosfera. Fonte: PEIXOTO; OORT (1992).
Referências
MAYS, L. W. Water resources engineering. [s.l.] John Wiley & Sons, Inc., 2005.
PEIXOTO, J. P.; OORT, A. H. Physics of climate. 1. ed. [s.l.] AIP-Press, 1992. p. 520
TRENBERTH, K. E. et al. Estimates of the Global Water Budget and Its Annual Cycle Using Observational and Model Data. Journal of Hydrometeorology, v. 8, n. 4, p. 758–769, 2007.
Note que os fluxos podem ser expressos em lâmina de água equivalente, dividindo-se o volume pelas áreas consideradas (Área da superfície da Terra = 510072000 km2, Área da superfície continental = 148940000 km2, Área da superfície oceânica = 361132000 km2).↩︎
Se esta fosse a única fonte de precipitação a média global da precipitação seria somente cerca de 233 mm, um valor típico de regiões semi-áridas e desertos.↩︎